魔方的分类

魔方有很多种，四面体魔方、镜面魔方、正方体魔方、粽子魔方等。
其中的一大类就是正多面体魔方。三维空间中的正多面体有五种：正四面体、正六面体、正八面体、正十二面体、正二十面体。那么魔方的形状只能从这五种形状里面选择吗？。答案是否定的，只要能够让立方体绕着轴转就可以，立方体也不一定是凸立方体，也不一定是正多面体。

总之，魔方就是可以改变状态的立方体。
每一个正多面体魔方都可以分为不同的阶数。例如：二阶正方体魔方、三阶正方体魔方、二阶正四面体魔方、三阶正四面体魔方等。
其中最常见的魔方就是正方体魔方，通常二阶魔方指的是二阶正六面体魔方。

魔方的状态

所有事物的状态都可以用一个向量来表达。魔方的状态也可以用向量进行表达，操作可以理解为置换。

魔方的操作集

魔方的操作组成的集合叫做魔方的操作集。
魔方的操作集常用的包括：最小操作集、完全操作集、最大操作集。
最小操作集是删除掉其中的任何一个操作都无法到达全部状态。
完全操作集指操作一步的情况下所能够执行的所有操作。
最大操作集：最小操作集中的每个元素进行扩充，达到它的全部周期。例如正方体的最大操作集是最小操作集元素个数的三倍，因为需要旋转3次才能够形成一个循环；四面体的最大操作集是最小操作集的两倍，等价于完备操作集，因为它的每个操作的周期是3。

置换

魔方的状态是一个向量，魔方的操作是一个置换。
魔方的操作如果可以作用于任何一个状态，那么它就具有很强的对称性。
正多面体魔方就是具有很强的对称性。在给定的状态下，我们可以执行完全操作集中的任何一个操作。
拼图的操作也是置换，比如N行M列的拼图，枚举空白所在的位置+可行的着法，可以得到很多个置换(大概略小于N*M*4)，拼图的置换就不是随意执行的，在特定的拼图状态下，只能执行很少的几种置换操作。

解魔方的过程等价于一个数学问题：给定一个置换集S，给定一个置换A，请尝试用S中的元素表示A。也就是把A分解为置换集中元素乘积的形式。

现在开始研究正方体魔方。
n阶正方体魔方由n^2-(n-1)^2个正方体小块组成，它有(n-1)*3种基本操作。固定魔方的最前，最右，最上角的一小块，可以执行下左后三类操作，每类操作有n-1种情况（表示转动几层）。

坐标系

魔方是三维空间中的立方体，三维空间有x，y，z三个轴，这三个轴分别用数字表示为0,1,2.

轴数字
x0
y1
z2

魔方的颜色

上下前后左右
白黄红橙绿蓝
用英语表示为white,yellow,red,orange,green,blue
简写为wyrogb
称之为"红心白发蓝右臂,黄足橙背绿左肩".

面颜色English
前面红色Red
后面橙色Orange
左面绿色Green
右面蓝色Blue
上面白色White
下面黄色Yellow

魔方的六个面

正方体有6个面,这是三维周正体的特点,二维中正方形4个边,四维中的周正体是正八体山.
这六个面分别以"前后左右上下"标识.
正方体可以展开成剑形:

  上  
左前右  
  下  
  后

"上左前右下后"分别编号为0,1,2,3,4,5

操作表示

对操作的编号=与该面垂直的轴的编号
对n阶魔方有三类操作：后，左，下。三类操作的编号分别为0,1,2.

x:0:后面旋转
y:1:左面旋转
z:2:下面旋转

操作序列举例：左2右3下2下下左左。左2表示旋转最左面的2层。这种操作序列表示法的好处在于可以表示任意一个n阶魔方。

魔方的操作

对于n阶魔方,固定离原点最远的那个小方块，则左边有n-1种旋转(只考虑单向旋转,因为逆向旋转可以通过三次单向旋转来实现),下边和后边也是有n-1种旋转. 这3*(n-1)种操作是最简操作集,最简操作集的意思是这些操作可以拼凑起其他操作,这些操作缺一不可,这就有点像矩阵里面秩的概念,矩阵的其他列向量都可以被基向量表示.
即对于n阶魔方,最简操作集包含3*(n-1)种操作,之所以是3是因为这是三维空间中的正方体,有下左后三个部分.如果是二维空间，则有下左两个部分。
当n=2时,最简操作集包含3种操作:左旋转,后旋转,下旋转.
相对于最简操作集,就有完备操作集.最简操作集和完备操作集都是不唯一的, 完备操作集包含的操作个数是最简操作集的二倍.
对于二阶魔方,至多有6种操作.顺时针右旋转相当于逆时针左旋转,所以二阶魔方的完备操作集为(顺+逆)*(左+后+下).
对于n阶魔方,把它的最简操作集加上顺逆即可构成完备操作集.例如三阶魔方最简操作集为6,完备操作集为12.最简操作集的一个例子为:上下前后左右六种顺时针选装.完备操作集的例子为(上下前后左右)*(顺逆).

n阶魔方的的属性

  • 方块个数：n^2-(n-1)^2

  • 颜色面数：n^2*6

  • 基本操作个数: 3*(n-1)

  • 状态个数：
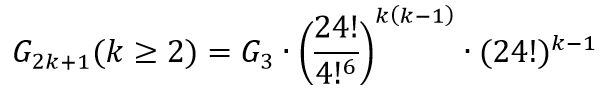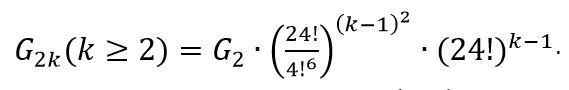
    奇数阶魔方状态总数 奇数阶魔方状态总数 偶数阶状态总数 偶数阶魔方状态总数

  • 上帝之数：上帝之数跟操作集有关，目前广泛认同的上帝之数都是在完备操作集上。二阶魔方6种操作上帝之数是12，三阶魔方12种操作上帝之数是19。二阶魔方上帝之数可以暴力求解，因为二阶魔方的状态数很少，三阶魔方的上帝之数人们花了三十年才通过精巧的设计求出来，四阶魔方的上帝之数至今未知。

全色魔方

面魔方只考虑魔方的六个面，而不考虑魔方体内不可见的小方块，以上讨论的都是面魔方。
全色魔方认为魔方体内有小方块，这些小方块也是有颜色的。二阶魔方体内肯定没有小方块，三阶魔方体内的小方块是固定的，四阶魔方体内有一个二阶魔方，五阶魔方体内有一个三阶魔方。
全色魔方
全色魔方虽然不太直观，但是却是理论上很美观，实际上也可以制作的，利用镂空或者透明的方法就能看到里面的小魔方。面魔方跟全色魔方在二阶和三阶上是等价的。

正方体与内存表示的等价性

在计算机中，二维数组、三维数组等都可以理解为正方形、正方体。Python中的张量就是一个N维向量，而N维向量就可以理解为高维空间中的长方体。
二阶魔方相比二阶四面体魔方要简单一些，二阶四面体魔方编程解决起来略微复杂一点。

了解魔方状态总数的意义

了解魔方状态总数可以了解魔方变化中的守恒量。
知道了魔方中的守恒量，就能够很快判断一个给定魔方是否有解。
了解了魔方中的守恒量，就能够知道最难状态的魔方。

二阶魔方状态总数

二阶魔方固定最右最上最前那一块之后，剩下7块随机排列，状态也随意，每个块有3种状态。但是最后一块的状态是确定的，可以跟据已经排好的前6块的状态确定，所以分母上除以3.

二阶魔方状态总数为7!*3^7/3=3674160

三阶魔方状态总数

三阶魔方在二阶魔方基础上多了心块和棱块。心块有24种放法，棱块有12块，最后两块的位置是固定的（分母除以2），最后一块的状态是固定的（分母除以2）。

三阶魔方状态总数为二阶魔方状态总数*24*12!*2^12/4=43252003274489856000

n阶魔方状态总数

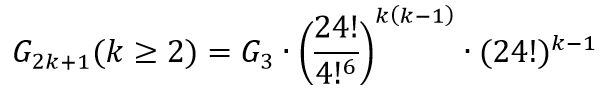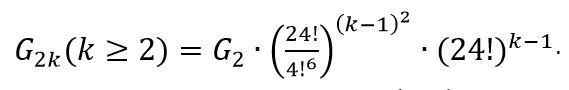
奇数阶魔方状态总数 奇数阶魔方状态总数 偶数阶状态总数 偶数阶魔方状态总数

从魔方状态总数中，可以发现魔方旋转过程中的守恒量。
二阶魔方和三阶魔方比较特殊，它们是最小的偶数阶魔方和最小的奇数阶魔方。
魔方中有以下五类块，这五类块组成了魔方状态的五个项。

  • 角块：角块就是一个二阶魔方，角块组成了魔方的骨架。
  • 心块：6个面，每个面有一个心，只有奇数阶魔方才有心块，偶数阶魔方没有心块。心块指的是魔方每个面的中心。
  • 面块：面上除心块以外的全部块，面块只有一个面颜色可见。魔方每个面上有4个块在同一轨道上，整个魔方每个轨道有24个块。同一轨道上的块是完全可以全排列且状态自由。
  • 边块：棱上除棱心以外的块，每个边块有两个面颜色可见。正方体有12条边，每条边上有两个对称的块，它们在同一轨道上但是它们并不等价。
  • 边心块：只有奇数阶魔方才有边心块。

参考资料

知乎：如何计算魔方状态总数
知乎：n阶魔方有几个等价类

六面异色正方体的24种放置方法

一阶魔方就是一个六面异色正方体，它有多少种放置方法？
首先，着地的面有六种情况。然后，固定着地面之后，前左右后四个面任意一个面都可以朝前，所以有24种防止方法。
相当于有24个结点的一个图,每个结点相当于一个状态.每个状态可以通过将最前面的这个面向上,向下,向左,向右旋转得到其他状态.即每个结点有4个邻结点.
于是给你出一道题,构造一个24个结点的图,使图中每个结点都与其它另外4个结点相邻.
这样的图是否唯一?
24个结点状态转移不一定通过4条边,也可能通过2条边.即向下,向右两种操作足以衍生出这4种操作.也就是说,在这向上下左右旋转四种操作这个集合有所冗余.它的原子操作是向右向下.向左旋转一次等价与向右旋转三次。
一个小正方体，各面异色。怎样描述这个正方体的状态呢？
只需要描述这个正方体红色面、蓝色面的朝向就可以了。
称这种状态描述法为x-y描述法。
这个小正方体有多少种状态呢？
红色有6种，每种红色固定后，蓝色有4种变化。所以共有24种状态。 状态之间是如何相互装换的呢？
每个状态结点有2个邻居结点：正对着你的这个面向下转和向右转，这是最小操作集。最大操作集是4：正对着你的这个面上下左右转动。
如何表示一个状态?法一用两个0-6之间的数字表示;法二用一个0-24之间的整数表示,x/6和x%6表示红面和蓝面所在的面的编号.

魔方整体旋转的位置

当向下旋转时,每一个小正方体都要发生位置改变,改变的是x-z平面,y坐标不变.
(x,y,z)变为(n-1-z,y,x),相当于左旋操作1
当向右旋转时,每一个小正方体都要发生位置改变,改变的是x-y平面,z坐标不变.
(x,y,z)变为(y,n-1-x,z),相当于下旋操作2

魔方后左下旋转时位置变化

n阶魔方： 当后旋时,op=0
(x,y,z)->(x,n-1-z,y)
当左旋时,op=1
(x,y,z)->(z,y,n-1-x)
当下旋时,op=2
(x,y,z)->(n-1-y,x,z)

魔方整体旋转的状态

当向下旋转,op=0时,y方向守恒，x和z方向交换
2->0
1->1
0->2
当向右旋转时,op=1时，z方向守恒，x和y方向交换
0->1
1->0
2->2,
也就是给定6个点求一个表达式newState=f(op,oldState)

opoldstatenewstate
020
011
002
101
110
122
即为newState=(5-op-state)%3

魔方后左下操作状态改变

当后旋时,op=0
0->0
1->2
2->1
当左旋时,op=1
0->2
1->1
2->0
当下旋时,op=2
0->1
1->0
2->2
即为newState=(6-op-state)%3

魔方整体操作和旋转操作之后的化简

魔方整体操作和旋转操作混合的序列形如：D后后2R左左
其中D表示向下，R表示向右
给定一个带有整体操作的操作序列，化简它的目的就是把全部D，R消掉，只剩下标准操作。
化简的原则如下：

{"D后(\\d*)", "下$1D"},
{"D左(\\d*)", "左$1D"},
{"D下(\\d*)", "后(N-$1)DR"},
{"R后(\\d*)", "左(N-$1)DDDR"},
{"R左(\\d*)", "后$1R"},
{"R下(\\d*)", "下$1R"},
{"[RD]*$", ""},
{"[RD]*", "simplify"}//对若干个RD执行化简操作

整个过程就像上下文无关文法逐渐推导一样，最终直到无法化简为止。

二阶魔方和三阶魔方是简单的，因为给定一个小块，可以很容易知道它应该去的位置。
四阶魔方中有些小块只有一个面是可见的，如何确定这些单面小块的状态呢？

如果使用6×n×n颜色表示法表示魔方，则可以直接模拟n阶魔方。

编号示意图

二阶魔方编号示意图

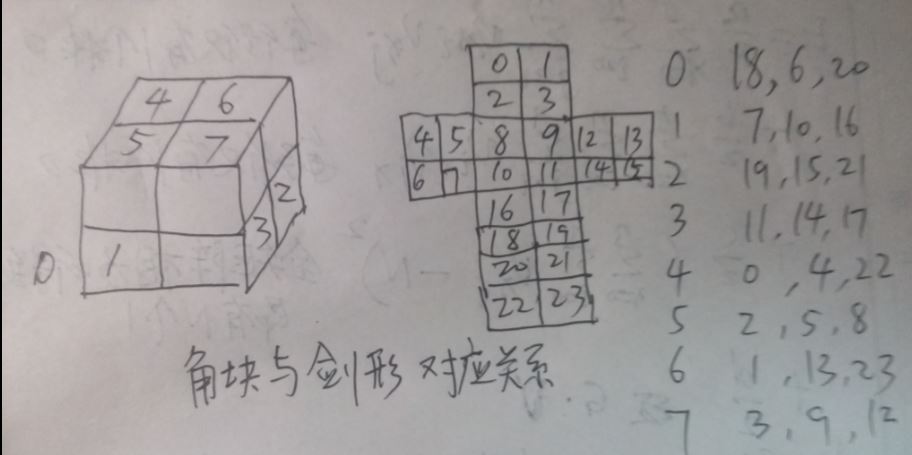
固定最上最前最右小方块

对于魔方,不转动它,可以有4*6=24种放置方法,这24种放置方法对应的是同一个魔方状态.
为了归一化,把红蓝白角块置于最前最上最右位置.这样一来,其余小方块全排列7!,其余小方块的状态为3^6,即最后一个小方块是不自由的,它的状态是由其余7个小方块决定的.
那么给定6个小方块的状态,如何求第七块小方块的状态?

小方块的状态定义

每个小方块有三种状态:0,1,2.每个小方块必然包含红面，魔方包含的每个小方块都是一个六面体，即便它的红色是隐藏的，它实际上也是有红色面的.
红面可以垂直于x轴或者y轴或者z轴,垂直于x轴称为0态,垂直于y轴为1态,垂直于z轴为2态.

小方块的位置定义

以最下最左最后那个小方块为原点,表示为(0,0,0),以从后往前为x轴,以从左往右为y轴, 以从下往上为z轴建系.可以为每一个小方块确定一个(x,y,z)坐标.

  • 0,0,0=0 黄橙绿
  • 1,0,0=1 黄红绿
  • 0,1,0=2 黄橙蓝
  • 1,1,0=3 黄红蓝
  • 0,0,1=4 白橙绿
  • 1,0,1=5 白红绿
  • 0,1,1=6 白橙蓝
  • 1,1,1=7 白红蓝

这样就为每个位置进行了编号,同时也为每个小方块进行了编号. 为颜色进行编码,设6个未知数r,y,w,g,o,b. 则按照上面各个小块的编码有:

  • y+o+g=0
  • y+r+g=1
  • y+o+b=2
  • y+r+b=3
  • w+o+g=4
  • w+r+g=5
  • w+o+b=6
  • w+r+b=7

这是一个6元线性方程组,它的秩为4,它的通解为 (r,y,w,g,o,b)=(1,2,6,-2,0,0)+k1(0,1,1,-1,0,-1)+k2(-1,1,1,0,-1,0) 为了使颜色区分开来,不能让orange和red与其它颜色相同.故可取k1=3,k2=0,得(1,5,9,-5,0,-3)，此法可以迅速跟据颜色找到小块的编号。

魔方24色表示法

将魔方展开成剑形,从左到右,从上到下写出24个小面的颜色,字符用wrgoby表示,或者用红黄蓝绿橙白表示.(不一定按照红心白发蓝右臂方式展开,程序可以自动调整成红心白发蓝右臂). 这种表示法存在很多冗余,但这种冗余可以作为校验,用来检验输入是否正确.

魔方的位置-状态表示法

在0~7七个位置,找到在该位置的小方块的编号,状态.这种表示法需要8个小方块的编号和状态,共需要16个数字.
还有另一种表示方法,知道了各个小方块的编号,用八个数字表示第0号,第1号...小方块的位置编号,另外8个数字表示第0号,第1号...小方块的状态.这种表示方法也是只需要16个数字.
后面这种方法更好,在状态转移过程中更容易计算,因为它关注的是每个小方块,而不是哪个位置上是谁.做变换时只需要考虑当前一个小方块的感受就可以了,不要考虑全局小方块. 比如,前一种方法在表示左旋,下旋,后旋时,需要考虑左面四块位置互换和状态改变,这个操作类似于将0,1,2,3变为1,2,3,0,即4个数字循环替换.
后一种表示方法只需要考虑每个小方块在该操作下发生的改变即可.
状态表示不同,深刻影响编程复杂度.本程序使用后一种表示方法.

魔方的最简表示法

固定了魔方的最上最前最右小方块,需要7个位置编号,6个状态编号.

打表用时11秒.
最简操作集左下后上帝之数为19
完备操作集上帝之数为12
3^19=1162261467
6^12=2176782336,这个数比int的最大值2147483647略大
如果用最暴力的方法,最简操作集搜索空间比完备操作集搜索控件小一半

魔方状态守恒量

固定最右最上最前块之后,其它块位置为全排列7!.状态却是3^6, 这说明其余6个块的状态决定了最后一个块的状态.
那么给定0~5小方块的状态共6个数字,如何求第6个小方块的状态.
这个问题等价于魔方掉了一个小方块之后，怎样才能正确安上？

只需要考虑相邻两块的状态变化族： 00、11、22是一家子
01、12、20是一家子 02、21、10是一家子
应用上式就可以对给定序列进行消元。

二阶魔方状态数

367,4160=7!*3^6  
7!=5040  
3^6=729  
6543210(7)=80,0667  
222222(3)=728

二阶魔方的状态数相当小,不过是三百六十七万个状态,数组完全可以存下. 如果一个状态用一个int值表示,那么需要空间3675160\*4B(大约14M)空间.

魔方求解手动公式

二阶魔方只需要两个公式就一定能够还原.

改变相邻两个块的状态

改变0,1两块的状态,不改变位置,应用下面的公式三次则恢复到原来的形状 76个公式

下后下下后下下左左下左后后后左后后后    
左后下下左左后下左左下下左后左后后后    
下后左左左下后左下后后左下左左后后后    
下后左左左下下后左后后下左下左后后后    
后左下后后下下左后后左下后后后左后后    
下后后下左后后后左后后后下后左左后后    
左下后后后下后后后左下后后下左左后后    
下下左下左左左后下左下下左左下左后后    
后左左后下左下下下后下后后左左下左后    
后左左后下左左后后下左下下下左下左后    
后后下后后后左下后后下左左后后左下后    
后下左下下后后左后左左左下左后下下后    
后下左下左左左下左后后下下左后下下后    
下左左下下后下下后下后后后左下下下后    
后后下下后左后后后下后后后下左后后左    
下左左左下左下后后下下后左下下后后左    
左下下后下左左下下左后下后后后左后左    
后后后下后后后下左下下左左后左左后左    
左后下后后后下左左左后下左左下下后左    
后后后下下左下后后左下后左下下下后左    
后后后下左下左后后下后左左下下下后左    
下下左后后下下后左下下下左下下下后左
下后左左左下左左左下后左左后后下左左
后后下左下下左左下左后下下下左下左左
后左左左下后后后左后左左后左左下下左
下后后左左下后左左后后左下左下下下左
左下下下左后后后下左后后左左下后后下
下后左左下下左后下下下左后后后左后下
后后后下后下左左下下左后下下左左后下
左左后后下左后后左左后下后下下下后下
后后下下左后后左下后后后左后后后左下
左左下左下下下后左左左下左后后左左下
下后下后后后左后下左左下下左后左左下
左后后左下下后后下左后后后下左左左下
左下下下左左后下后后左后左下左左左下
左下下下左下后下后后左后下下左左左下
左后左左左后左后下下后后下左后后下下
左下下后后下左下下下后左左左下左下下
左后左左左后后下左下下后下后左后后后
左后左左左后左下左下下后下左左后后后
下后下下左左后下后后下下后下左后后后
左后下下后左左下下左后下下下左后后后
左左下左下下下后下左后后左左后下后后
后左后下下后后左后后左后左左左下后后
左后后左后左左左下后后后左后下下后后
下左后后后下左左左下左后后左下下后后
后左左后下后下下下后下左左后后下左后
后左左后下后后左左下左下下下后下左后
后后左下下下后下后后下后后左左后下后
后下左后左左左下左下下后后左后下下后
后下左后后下下左后左左左后左后下下后
左下下左左后下下后左下下下后下下下后
下左左左下后后后下后下下后后左后后左
左后左左下下左后左左左下后后后左后左
后后后下左后左左后后左后下下左左后左
下下后后左后左左后后左后左下下下后左
下后左左左下后下后后下下后下后后左左
下左左后后左后下下下后下下下左下左左
后后左左下后后下左下下下左后后后下左
下下左下左左左后左左左后下后后下下左
左后下后后后下后下左左下下左后下下左
下后后下后后左左后左后后后左下下下左
下左左左下左后下后后左后左左下下下左
下左左左下下后下后后左后下左下下下左
左下下下左下左后后左左后下左左后后下
后后左左后下后后后左下下下后下后后下
下左左后下左左下下左后左后后后左后下
后后后下左左左后下左左下下后左左后下
下后下后后后左下下下后下左左下下后下
后后后下后左后左左下左后后下下下后下
左左下后后左左后下左左左后下下下后下
后后后下下左后左左下左下后下下下后下
左后后下下左后下下后后下左下左左左下
后左左左后左左左下后左左后下下左左下
左后左左左后下下下左后下下后后左下下
后后左后下下后后下左后左左左下左下下

改变相邻两块的位置

改变0,1两块的位置,不改变状态

下后下下后左后后左下左后后后左
下后下下后左左后下后左左后后左
下后后下左下后后后左下左后后左
左后下左后后左后后左下左后后左
下后下左下后左后后左下左后后左
下下左下后左左后后左下左后后左
下后下下后左后下后左下左后后左
下后下下下左后下左左下左后后左
下后下下后后下后左下下左后后左
下后后下左左下后左后后左左后左
下后后后下左下后后下后左左后左
下后后下左下后左后下后左左后左
左后下左后后左左后下后左左后左
下后下左下后左左后下后左左后左
下下左下后左左左后下后左左后左
下后后下下后左后下下后左左后左
下后后下左下下左后下左左左后左
下后下左左下后左后后左下左后左
下后后下左下后后下后左下左后左
左后下左后后左后下后左下左后左
下后下左下后左后下后左下左后左
下下左下后左左后下后左下左后左
下后下下后左后下下后左下左后左
左后下左左下左后左左左下左后左
左后后左后下后后下左左下左后左
左左下左后左左后下左左下左后左
左后下左后下左后下左左下左后左
下后下左下下左后下左左下左后左
左后下下后下左下下左左下左后左
下下左左下后左后后左下下左后左
左后下左后后后下后左下下左后左
下后下左下后后下后左下下左后左
下下左下后左后下后左下下左后左
下下下后左后下下后左下下左后左
下下左下下左后下左左下下左后左
下下左下后后下后左下下下左后左
下后下左左下后左左后下后左左左
下后下左左左下后左后后左下左左
下后下左左下后左后下后左下左左
下后后下左下后后下下后左下左左
左后下左后后左后下下后左下左左
下后下左下后左后下下后左下左左
下下左下后左左后下下后左下左左
下后下下后左后下下下后左下左左
下后下左左下下左后下左左下左左
下后下左左下后后下后左下下左左
左后下下后下左左下后左后后后下
左后下下后后下左下后后下后后下
左后后左后下后后后左后下后后下
左左下左后左左后后左后下后后下
左后下左后下左后后左后下后后下
下后下左下下左后后左后下后后下
左后下下后下左下后左后下后后下
左后下下下左下后左左后下后后下
左后下下后下下后左后下下后后下
左后后左后后左下左后后左左后下
左后后左左后下后左左后左左后下
左后后左后下后左下左后左左后下
左左下左后左左左下左后左左后下
左后下左后下左左下左后左左后下
下后下左下下左左下左后左左后下
左后后后下后左下下左后左左后下
左后后左后下下后左下左左左后下
下后下左左下后左后后后下左后下
下后后下左下后后下后后下左后下
左后下左后后左后下后后下左后下
下后下左下后左后下后后下左后下
下下左下后左左后下后后下左后下
下后下下后左后下下后后下左后下
左后下左左下左后左左后下左后下
左后后左后下后后下左后下左后下
左左下左后左左后下左后下左后下
左后下左后下左后下左后下左后下
下后下左下下左后下左后下左后下
左后下下后下左下下左后下左后下
左左下左左下后下左左下下左后下
左左左后左下后后下左下下左后下
左左下左后左下后下左下下左后下
左后下左后下下后下左下下左后下
下后下左下下下后下左下下左后下
左左下下左后左下下左下下左后下
左左下左后后左下后下下下左后下
左后下左左下左左下后下左左下下
左后下左左左后左下后后下左下下
左后下左左下左后左下后下左下下
左后后左后下后后下下后下左下下
左左下左后左左后下下后下左下下
左后下左后下左后下下后下左下下
下后下左下下左后下下后下左下下
左后下下后下左下下下后下左下下
左后下左左下下左后左下下左下下
左后下左左下左后后左下后下下下

总状态数

3674160

最简操作集各个步数对应的状态数

0 = 1
1 = 3
2 = 9
3 = 27
4 = 78
5 = 216
6 = 583
7 = 1546
8 = 4035
9 = 10320
10 = 25824
11 = 62832
12 = 146322
13 = 321876
14 = 635632
15 = 988788
16 = 958176
17 = 450280
18 = 66420
19 = 1192

完备操作集步数对应的状态数

6种操作，上帝之数为14.

1=>6
2=>27
3=>120
4=>534
5=>2256
6=>8969
7=>33058
8=>114149
9=>360508
10=>930588
11=>1350852
12=>782536
13=>90280
14=>276

9种操作：包含旋转180度

左右下三种操作，分别执行1次、2次、3次，一共9种操作。

1=>9
2=>54
3=>321
4=>1847
5=>9992
6=>50136
7=>227536
8=>870072
9=>1887748
10=>623800
11=>2644

步数与状态数之间是否存在数学表达式的关系

状态数=f(步数)，能否求出f的表达式.

三阶四面体魔方有75582720种状态，但是也有人说是933120种，正好是75582720的81分之一。原因是933120这种统计忽略了四个小角的状态。

最简操作集

以933120种状态为前提：
如果考虑最简操作集，只考虑四种操作，则三阶四面体魔方的上帝之数是21

1=>4
2=>13
3=>36
4=>99
5=>270
6=>736
7=>1981
8=>5197
9=>13127
10=>31217
11=>67496
12=>124400
13=>181994
14=>202529
15=>166615
16=>95521
17=>35521
18=>6122
19=>224
20=>14
21=>3

完全操作集

以933120种状态为前提：
如果考虑完全操作集，4*2等于8种操作，三阶四面体魔方的上帝之数是11。 

1=>8
2=>48
3=>288
4=>1728
5=>9896
6=>51808
7=>220111
8=>480467
9=>166276
10=>2457
11=>32

最大操作集

最大操作集与完备操作集一致，因为四面体魔方最小操作集中的每个操作周期为3.

最简操作集

三阶魔方最简操作集步数与状态数对应关系：

1=>6
2=>33
3=>180
4=>975
5=>5286
6=>28635
7=>155040
8=>839157
9=>4540668

完备操作集

最大操作集

0 1
1 18
2 243
3 3240
4 43,239
5 574,908
6 7,618,438
7 100,803,036
8 1,332,343,288
9 17,596,479,795
10 232,248,063,316
11 3,063,288,809,012
12 40,374,425,656,248
13 531,653,418,284,628
14 6,989,320,578,825,358
15 91,365,146,187,124,313
16 约1,100,000,000,000,000,000
17 约12,000,000,000,000,000,000
18 约29,000,000,000,000,000,000
19 约1,500,000,000,000,000,000
20 约490,000,000

全排列散列

位置是一个数组,将位置数组通过全排列散列映射到一个int值.在进行位置变换时,将int值解析成位置数组,变换完成后再将新数组映射到int值.这样很麻烦.能否不通过解压int直接进行位置变换？

打表法要义

从目的状态出发,进行广度优先遍历,用一个队列足矣.
广搜时状态转移为最简操作集的逆操作,这样才能保证输出结果是正操作.
比如6面异色正方体向下向右旋转,在从目标状态出发产生新状态时,要向上,向左操作. 向上向左产生的状态插入到状态队列中去.
从目的状态到x状态的序列为:上上左上.则从x状态返回目标状态就是下右下下.
对于逆操作,只需要通过改动数据表来实现.而数据表是无论如何无法避免的.
对于操作序列,可以用字符串表示,也可用int值表示.用int值表示时op=op<<1|0或者op=op<<1|1.  

其它思路

启发式搜索:如果无法前进也要后退.
投票搜索,8个人投票决定下一个操作是什么,像神经网络中的神经元一样.
双向广搜:从目标结点和源节点同时进行搜索,原来的3^19变成了2*3^9.
多点广搜,在魔方图中找到几个核心点,知道这些核心点怎么去目标结点,从这些核心点出发进行广搜.就像双向广度优先搜索一样.也就是说在地球表面均匀的建立几个基站, 这些基站都知道如何到达北极点.给定一个点,问它如何到达北极点时.从给定点出发进行广搜, 直到找到一个基站为止.因为基站的存在保证了对于地球上每一个点, 离他4步以内必然存在至少一个基站.这样一来就可以通过一次广搜找到基站, 从基站到北极点可以通过查表得到.

使用魔方求解器推断出来的魔方公式，只需要6个公式就能够还原魔方。

八个角块

八个角块构成一个二阶魔方。直接使用二阶魔方求解即可。 相邻块为0号块和1号块。
改变相邻块的状态

后后左后下下后后下左后左左左下左下下

改变相邻两块的位置，改变0,1两块的位置,不改变状态

下后下下后左后后左下左后后后左

6个心块

六个心块可以通过只旋转棱的方式快速达成。

左面的上右下三个块

三块可同时旋转，旋转过程中像刚体一样。 左面考察三个块，12为上，34为右，56为下。
状态只能同时变两块。不妨考虑改变上右两块的状态。
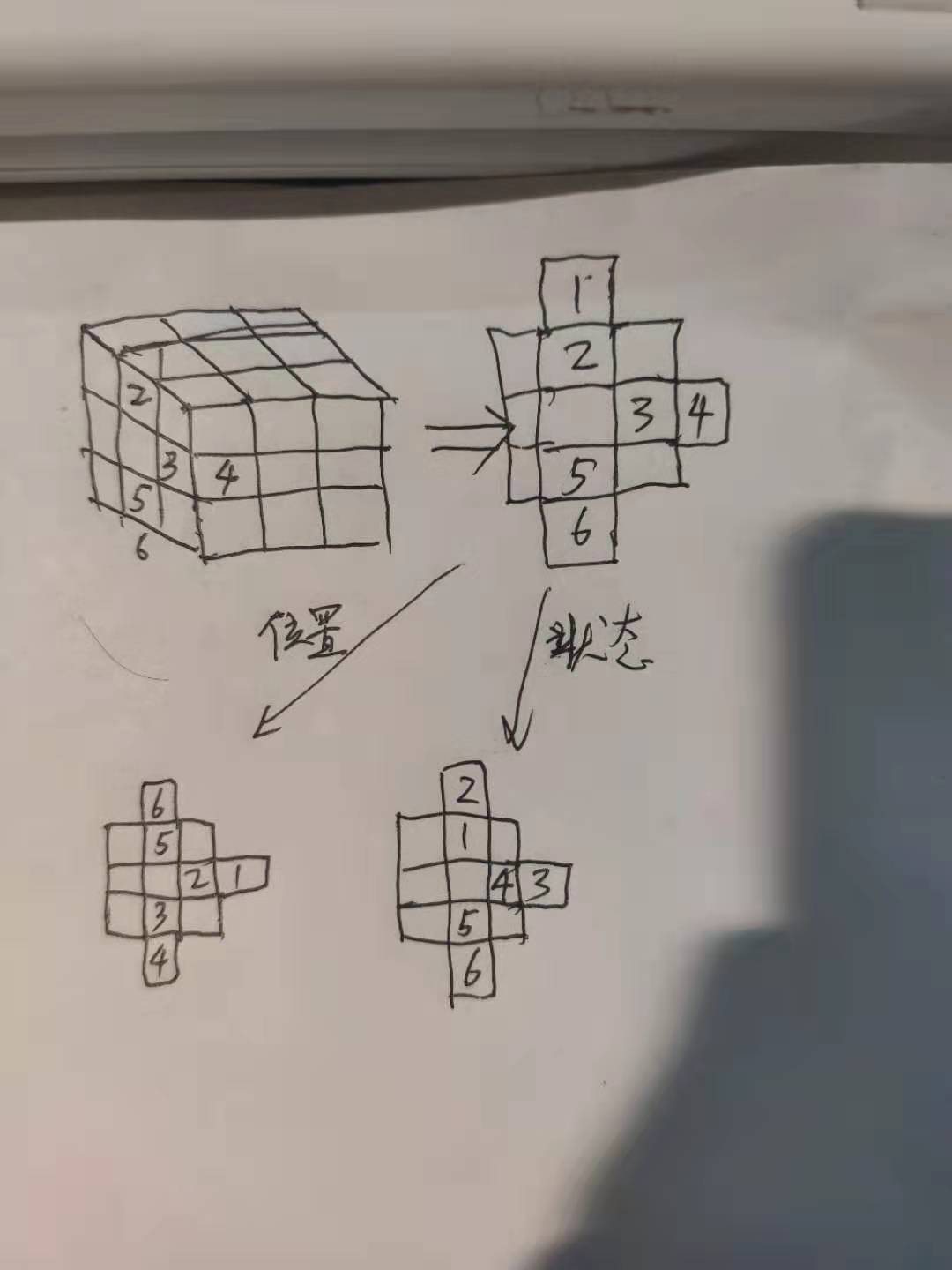
面上三个边块的变化示意图
改变左面的三个小块,三个小块顺序为:上右下 其中左面方块始终固定，不必考虑 交换上右两块的状态,不改变位置

后2下左2下下
左2左2左2
后2后2后2
左下下后2后2
左2左2下下
左2左2后2后2
下左左下

交换“上右下”三块的位置和状态，此操作周期为3（和二阶魔方状态公式一样）

后2后2后2后
左2左2左2
下2下2左下2下2下2下
左左左下2下2
左2后2后2后后

在左面固定的情况下，一共有： 上右下，这是完美状态，但是可能上右状态恰好相反 右下上：执行第一遍 下上右：执行第二遍 执行第三遍则编程上右下完美状态

三种合法位置。

角落三块

正方体有八个角，每个角对应3个边块。以最前，最左，最上那个角为研究对象。
魔方的角落三块变换法则：

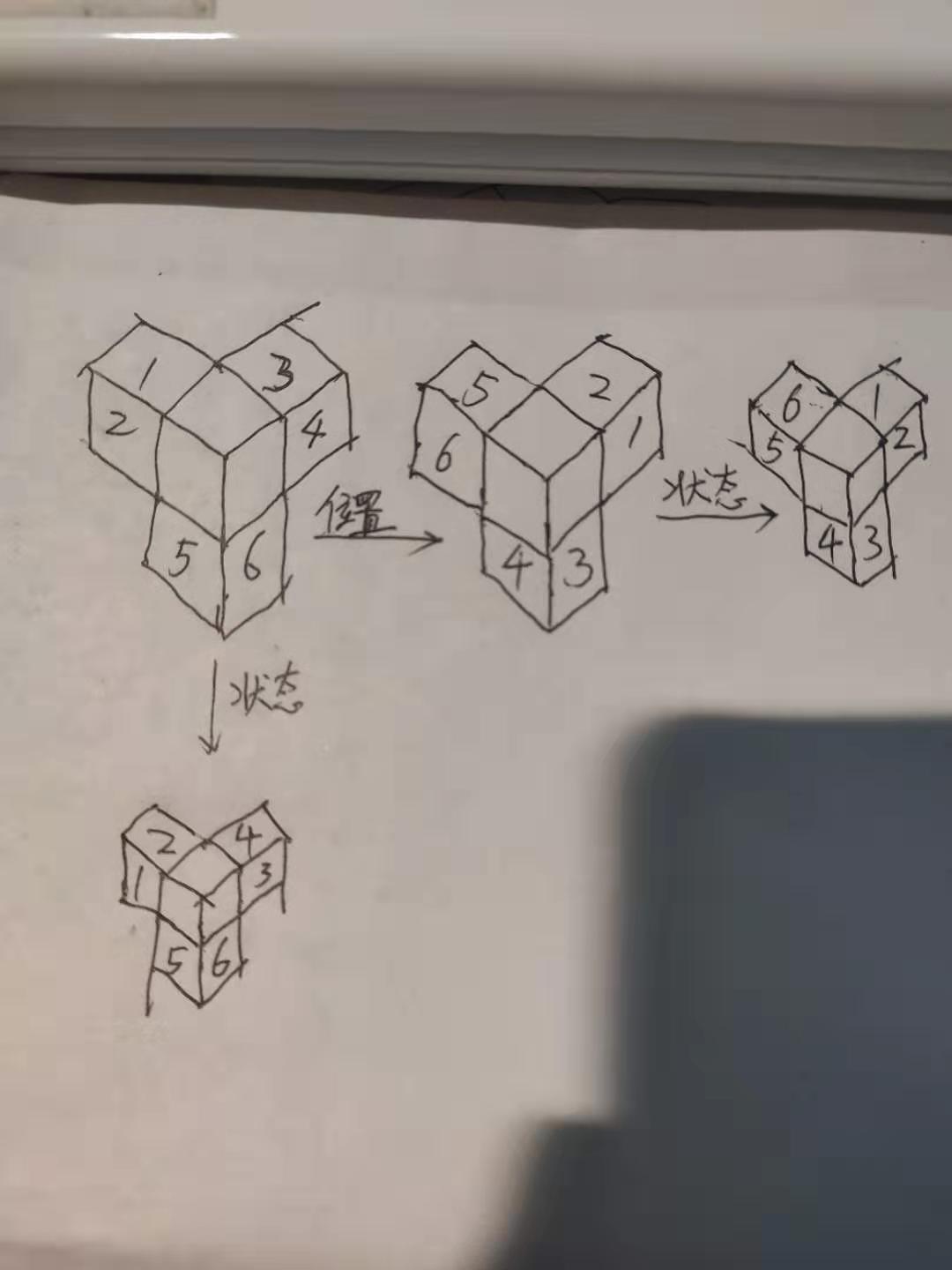
  • 角落发生顺时针或活着逆时针旋转，3个边块的颜色就像风扇一样维持不动 角落三块旋转示意图
  • 角落中的三块有两块可以同时变色（不能三块同时变色也不能只有一块变色）

改变状态不改变位置：改变顶面上两个边块的状态，下边那个边块完全不动。

左2左左左下下下
左左下左2左
下下下左2左2
后后左左下下下
左左后后下下下
左左下

改变三个块的位置，此操作周期为3。

后2后2左后2后2
下2下2后后
左后后下下后
下2下2后2后2后2
左2左2左左
后下2下2后2后2后2

使用以上六个公式可以实现三阶魔方的还原。

三阶魔方最简公式的缩写

基于最简公式，使用程序可以快速生成魔方的解法。但是它的缺点就是比较冗长。
基于搜索的方法，只搜索10层，然后可以得到置换向量，这就相当于得到了许多公式的缩写形式。

维基百科

四面体魔方的放置方法

一阶四面体魔方只有一块，它有4*3=12种放置方法。其中4表示4个面选择哪个面当做底面，3表示剩下的三个面选择哪个面当做正面。
将12种状态看做结点，每个结点有四种操作方法，绕着四个角转动：下、左、右、后。
这就形成了一个图，图中每个结点都有四条边，且每个顶点都是等价的。
这个图其实就是一个正八面体，也可以看做是正六面体的对偶图。

四面体魔方的状态总数

二阶四面体魔方有3*3*3*3种状态，顶块固定，三个角有各三种状态，最下面一层有三种状态。
或者可以认为中间块固定，只有四个角可以动，每个角各有三种状态。

三阶四面体魔方有75582720种状态，但是也有人说是933120种，正好是我给出的答案的81分之一。原因是933120忽略了四个小角的状态。

933120的计算方法：

Centers: 3^4
Edge permutation: 6!/2
Edge orientation: 2^5
3^4*6!*2^4=933120

给定置换集合，求置换群的大小。这个问题除了广搜深搜之外是否存在便捷的方法。

四面体魔方的本质

四面体魔方的4个角可以去掉，这样它就变成了一个异形魔方。
从四面体魔方的计数上也能够看出来。

四面体魔方的操作方法

顶部固定，转动四个角及层数+转动底部及层数，总共有4*(阶数-1)中操作方法。
正方体旋转和四面体旋转都是旋转面，并且面使用左手准则，大拇指指向体心到面心。
左面、正面、右面、下面，分别为0/1/2/3。

如果认为三阶四面体魔方的状态总数是933120，则只需要忽略转一层的情况。

四面体魔方的表示方法

魔方的操作其实就是置换，对于置换如果每次都手动去操作会非常复杂。并且对于更高阶的四面体魔方，同样希望快速产生操作对应的置换。
把四面体魔方看做一个一个的小四面体，每个小四面体有状态。当旋转的时候，让符合条件的小四面体绕着一个轴进行旋转，既改变小四面体的位置，又该改变小四面体的状态。
旋转完成之后，可以把立体映射成平面。
所以这就需要建立平面图与立体图之间的映射，操作的时候在立体上进行操作，渲染的时候在平面上进行处理。

在处理二阶魔方和三阶魔方的时候，之前一直对颜色看的比较重要，必须把魔方摆放成为红心白发蓝右臂的形式，然后输入。程序内部会把颜色直接映射成颜色的int值。
这种方式存在很多缺点：

  • 魔方的颜色不一定是按照规定的来，例如红色和橙色不一定是相反色，魔方的颜色也不一定在"红白蓝橙绿黄"这六种颜色里面选取。
  • 用户理解把魔方摆成”红心白发蓝右臂“存在一定的理解成本，无法快速学习。

那么如何解决这个问题呢？
对于正方体魔方，首先找到红心白发蓝右臂那个块，然后直接把白色置为0，红色置为2，蓝色置为3。剩下的任务就是寻找红白蓝三种颜色的对面。把正方体简化为八个角，也就是简化为一个二阶魔方。然后根据8个角来寻找对面，如果一个角包含红蓝两色，那么这个角剩下的那个颜色一定是白色的对面。利用这种三缺一的思路，可以找到红白蓝三种颜色的对面。

六轴魔方

一般魔方

二阶魔方，三阶魔方，四阶魔方，五阶魔方，六阶魔方，七阶魔方，九阶魔方

延伸

  • 魔球
  • 粽子魔方（三阶魔方变种）
  • 镜面魔方（三阶魔方变种）

四轴魔方

  • 钻石魔方
  • 金字塔魔方
  • 斜转魔方
  • Skewb Ultimate

八轴魔方

▪ Brain Twist

十二轴魔方

▪ 五魔方 ▪ 菊花五魔方 ▪ 亚历山大之星

其他魔方

▪ Square 1

衍生

这些衍生品已经不能称之为魔方了，而是一种新玩具。
▪ 鲁比克360 ▪ 魔板 ▪ 魔表 ▪ 魔尺

总结

魔方为了旋转性，它必须是正多面体，否则转不动。
三维空间中的正多面体只有5种：正4面体，正六面体，正八面体，正十二面体，正二十面体

n阶正k面体魔方最多包含n*(k-1)种操作。

n阶魔方的制作

理论上魔方有无数中，但若要造成实物则需要极其巧妙的机械设计。

七阶魔方由希腊Olimpic方块公司的设计师花费五年时间，数万欧元研制成功，其独具匠心的弧形设计一举打破了传统魔方的固定样式，同时兼备了收藏，鉴赏及实用价值。Vcube设计师的这一天才设计，终于克服了困扰魔方界的一大难题，魔方突破了六阶的极限，并为今后更高阶魔方的诞生指明了前进的道路，按此结构的制作魔方理论上可达11阶。由于魔方玩家的人数较少，Olimpic公司开始大力改进和生产七阶魔方，一段时间内是世界上唯一能生产七阶魔方的公司，人们不得不花费高额的价格从希腊订购。但随着魔方玩家的剧增，Vcube七阶魔方长期不更新和价格昂贵，国内外的其他公司也开始批量生产七阶魔方，虽有细节上的改进但基础结构仍基于Vcube七阶魔方的设计。如今，Vcube、中国的永骏二代7阶、蓝蓝七阶等品牌已经并驾齐驱，特别是中国新兴的这些生厂商，由于把资金投入在魔方细节的改善上，使得其七阶魔方的手感和顺滑度远远好于Vcube七阶魔方,越来越受到人们的青睐。但是不得不说的是，如果没有Vcube设计师的天才设计，世界上也许就不会出现高于六阶的魔方了，因此，对于这些设计师应给予最高的尊重。

参考资料

百度百科

https://baike.baidu.com/item/%E4%B8%8A%E5%B8%9D%E4%B9%8B%E6%95%B0/10098625

HalfSolver

二阶魔方在3种操作的情况下上帝之数是19，现在考虑它的一半操作。
执行10步所能够形成的全部置换，把10步之内所能够得到的置换全部存储起来。
当来一个问题的时候，等价于把这个问题对应的置换，分解为两个置换的乘积操作。

这种方式能够避免状态数过多导致的状态爆炸问题。实际上，这种方法就是双向广度优先搜索的变形，但是实现比广度优先方法要灵活许多。

空间复杂度较低，时间复杂度略高。
同样，使用这种方法还可以实现把一个置换拆分成3份，这样空间复杂度会进一步降低。

这种算法等价于：把比较少的基本操作需要很多步才能完成，转化为了比较多的基本操作需要很少的步完成。是一种用时间换空间的策略。

获得了很多个操作之后，可以使用A*算法贪心搜索让尽量多的块实现复原。但是可能存在一些问题，使用A*计算量太大。

搜索n层，然后将问题对应的置换分解为三个置换的乘积。如果直接硬搞，复杂度是N*N,N表示搜索n层之后的全部置换种数。为了降低复杂度，第一步使用启发式搜索，优先选择离目标尽量近的一种操作，然后通过O(N)复杂度判断是否可解。

三阶魔方能够解决18步以内可以解决的东西。把三阶魔方的还原分成几个步骤：第一步，把底层还原；第二步，把中间层还原；第三步，把上层还原。只要每一步都可以在18步内解决，那么魔方就能够被还原。合理指定小目标，确保每个小目标都能够在特定步骤之内还原，这样问题就变得迎刃而解。
这种方法几乎是万能的，把一个大目标拆解为若干个小目标，然后确保每个小目标能够实现。

三阶魔方最简操作方式，使用6层打表搜索2步的SearchSolver，解决随机旋转5步的问题，在很多时候是不成功的。因为随机旋转5步是正向旋转5步，如果正向旋转5步，那么要想使用正向操作还原它的时候，可能需要15步才能还原它。所以可以把搜索步数改为3步，或者把打表层数改为8层。

start模式

一个魔方状态可以用颜色块进行表示，比如正方体魔方有6个面就用6种颜色表示，四面体魔方有4个面就用4种颜色。称这种形式为颜色模式。
一个魔方的状态也可以用向量进行表示，把魔方展开成平面形状，然后从0开始进行依次编号。称这种表示形式为start模式。
二阶魔方和三阶魔方都很容易实现颜色模式和start模式的转换，因为二阶魔方和三阶魔方中没有重复块，每个块都是独一无二的。把二阶魔方、三阶魔方涂上颜色与标注数字是一样的。只需要建立小块与平面展开的ID的映射关系即可。
但是三阶四面体魔方存在很多重复的小立体，四阶六面体魔方也存在很多重复小立体，建立start模式和颜色模式的互相转换可能并不那么容易。
start模式下的问题要比颜色模式下的问题难。只是在阶数较低的时候start模式和颜色模式有重合。

HalfSolver

魔方需要n步才能还原，搜索n/2步，建立table。
给定问题的状态，对它施加table中的一个动作，得到中间状态，对中间状态直接求把它还原的置换，从table中把这个置换找出来。
有了置换就有了operation。

GreedySolver

HalfSolver需要n/2步，table依旧太大。
魔方需要n步还原，打标n/k步，建立table。
给定问题的状态，使用贪心的方式，对每个状态建立一个评价机制，得到它的goodness。
对于table中的每个操作，执行之并计算goodness。优先执行goodness最高的操作。
但是这样可能会产生循环，为了避免状态不变，附加一条标准：执行操作之后不能与已经出现过的状态重复。 这种方法得到的解法会比较长。

SearchSolver

为了解决GreedySolver步骤太多、答案太长的问题，提出了SearchSolver。出发点在于：魔方需要n步还原，打表n/k步，那么最多需要k层搜索就能够找到答案。
SearchSolver是一种递归的搜索方式，对于每种状态，对它执行table中的每一种着法，然后评价goodness，将操作按照goodness进行降序排序。然后依次执行各个操作，执行完每个操作之后，递归执行以上过程。
为了加速SearchSolver，在最后一层搜索的时候，直接判断是否存在一步置换就能还原的情况。

SearchSolver可以替代HalfSolver和GreedySolver

SearchSolver其实是可以替代HalfSolver和GreedySolver。 SearchSolver搜索两层就是HalfSolver。
SearchSolver搜索深度无限大，每一层的搜索宽度设置为1，就是GreedySolver。

实现网页版，根据几张图片推导推导魔方初始状态，从而给出解法。难点：颜色等价（不同魔方可能颜色不太一样，不能把颜色写死，而要通过聚类的方式得到六种颜色）。视觉模块分为识别每个小面、识别大面之间的相对位置、转化为剑形输入三个模块。

暴力解决三阶魔方的12个边块

三阶魔方的八个角块可以像二阶一样去解决，只需要找到不改变角块时边块的操作方法，就能够找到一种解决三阶魔方的方法。
fac(12)*4096 1961990553600=1827G

寻找上帝之数

1992 年， 德国数学家科先巴(H. Kociemba) 提出了一种寻找魔方复原方法的新思路。 他发现， 在魔方的基本转动方式中， 有一部分可以自成系列， 通过这部分转动可以形成将近 200 亿种颜色组合。 利用这 200 亿种组合， 科先巴将魔方的复原问题分解成了两个步骤： 第一步是将任意一种颜色组合转变为那 200 亿种组合之一， 第二步则是将那 200 亿种组合复原。 如果我们把魔方复原比作是让一条汪洋大海中的小船驶往一个固定的目的地， 那么科先巴提出的那两百亿种颜色组合就好比是一片特殊的水域 - 一片比那个固定地点大了 200 亿倍的特殊水域。 他提出的两个步骤就好比是让小船首先驶往那片特殊水域， 然后从那里驶往那个固定的目的地。 在汪洋大海中寻找一片巨大的特殊水域， 显然要比直接寻找那个小小的目的地容易得多， 这就是科先巴的新思路的优越之处。但即便如此， 要用科先巴的方法对 “上帝之数” 进行估算仍不是一件容易的事。 尤其是， 要想进行快速的计算， 最好是将复原那 200 亿种颜色组合的最少转动次数 (这相当于是那片 “特殊水域” 的地图) 存储在计算机的内存中， 这大约需要 300 兆的内存。 300 兆在今天看来是一个不太大的数目， 但在科先巴提出新思路的那年， 普通机器的内存连它的十分之一都远远不到。 因此直到三年后， 才有人利用科先巴的方法给出了第一个估算结果。 此人名叫里德(M. Reid)， 是美国中佛罗里达大学(Unversity of Central Florida) 的数学家。 1995 年， 里德通过计算发现， 最多经过 12 次转动， 就可以将魔方的任意一种颜色组合变为科先巴那 200 亿种组合之一； 而最多经过 18 次转动， 就可以将那 200 亿种组合中的任意一种复原。 这表明， 最多经过 12+18=30 次转动， 就可以将魔方的任意一种颜色组合复原。 这些计算结果表明， “上帝之数” 不会超过 26。 但是， 所有这些计算的最大优点 - 即利用科先巴的那片 “特殊水域” - 同时也是它们最致命的弱点， 因为它们给出的复原方法都必须经过那片特殊水域。 可事实上， 很多颜色组合的最佳复原方法根本就不经过那片特殊水域， 比如紧邻目的地， 却恰好不在特殊水域中的任何小船， 显然没必要故意从那片特殊水域绕一下才前往目的地。 因此， 用科先巴的思路得到的复原方法未必是最佳的， 由此对 “上帝之数” 所做的估计也极有可能是高估。 可是， 如果不引进科先巴的特殊水域， 计算量又实在太大， 怎么办呢？ 数学家们决定采取折衷的手段， 即扩大那片特殊水域的 “面积”， 因为特殊水域越大， 最佳复原路径恰好经过它的可能性也就越大 (当然， 计算量也会有相应的增加)。 2008 年， 研究 “上帝之数” 长达 15 年之久的计算机高手罗基奇 (T. Rokicki) 运用了相当于将科先巴的特殊水域扩大几千倍的巧妙方法， 在短短几个月的时间内对 “上帝之数” 连续发动了四次猛烈攻击， 将它的估计值从 25 一直压缩到了 22。这是当时全世界范围内的最佳结果。 罗基奇的计算得到了电影特效制作商索尼影像 (Sony Pictures Imageworks) 的支持， 这家曾为 “蜘蛛人” 等著名影片制作特效的公司向罗基奇提供了相当于 50 年不停歇计算所需的计算机资源。 与此同时，科学家们发现了一种已知的最混乱状态——superflip。在Superflip这种状态中，每个魔块的位置都是对的，除了每个棱块都是翻转反向的。这种形态已被证明不可能用小于20种方法还原，因此上帝之数一定大于等于20，也有不少的研究人员预测，上帝之数就是20。 2010年7月，美国加利福尼亚州科学家征用到了更加强大的资源——谷歌旧金山总部的超级主脑计算机。随着程序的精简和设备的提升，这量配置惊人的计算机破解了这一谜团。研究人员利用计算机，用枚举法验证了每一种情况，证明任意组合的魔方均可以在20步之内还原，“上帝之数”正式定为20。 这支研究团队位于美国加利福尼亚州帕洛阿尔托市。科学家们通过计算机计算和证明，任意组合的魔方都可以在20步内还原。这一结果表明，大约有10万多种的起始状态恰好可以在20步内还原。 利用谷歌公司计算机强大的计算能力，研究人员检验了魔方任何可能的混乱状态(确切数字为43,252,003,274,489,856,000约合4.3×10的19次方)。美国俄亥俄州肯特州立大学数学家莫雷-戴维德森教授也是研究人员之一，他表示，“我们现在可以肯定，这个‘上帝之数’就是20。对于我来说，我也回到了原地。魔方伴随着我成长，这也是我为什么深入研究这个数学问题的原因。这个谜团引起了人们的广泛关注，它也许是人类历史上最受欢迎的谜语了。”科学家们的初步研究成果发表于在线网站上，但戴维德森表示，他们准备将研究成果提交给杂志正式发表。 程序员托马斯-罗基花了15年的时间，致力于寻找这个谜团的答案。据罗基介绍，研究团队所采用的算法可以在1秒钟内尝试10亿种可能，此前的计算机算法1秒钟内只能处理4000种可能。 为了让问题简单化，研究团队采用了一种所谓“群论”的数学技术。他们首先将魔方所有可能的起始状态集分成22亿个集合，每个集合包含了195亿个可能的状态。集合的分配原则是这些可能的状态是如何应对一组10个可能的还原步骤。再通过魔方不同的对称性，这种分组技术使得研究团队将集合数减少到5600万个。 研究人员所采用的算法可以快速将这些还原步骤与恰当的起始点匹配起来，从而实现在20秒内处理一个集合中的195亿种可能。对于普通的家用电脑来说，以这样的速度完成整个处理任务需要大约35年时间。

魔方与数学

1974 年春天，匈牙利布达佩斯应用艺术学院(Budapest College of Applied Arts) 的建筑学教授鲁比克(E. Rubik) 萌生了一个有趣的念头， 他想设计一个教学工具来帮助学生直观地理解空间几何的各种转动。 经过思考， 他决定制作一个由一些小方块组成的， 各个面能随意转动的 3×3×3 的立方体。 这样的立方体可以很方便地演示各种空间转动。 随后魔方风靡全球， 其原因最大的魔力就在于其数目惊人的颜色组合。 一个魔方出厂时每个面各有一种颜色， 总共有六种颜色，（一般为 ：黄、白、绿、蓝、红、橙） 但这些颜色被打乱后， 所能形成的组合数却多达 4325 亿亿个（注意确实是两个亿字）。 如果我们将这些组合中的每一种都做成一个魔方， 这些魔方排在一起， 可以从地球一直排到 250 光年外的遥远星空。 也就是说， 如果我们在这样一排魔方的一端点上一盏灯， 那灯光要在 250 年后才能照到另一端。 如果哪位勤勉的玩家想要尝试所有的组合， 哪怕他不吃、 不喝、 不睡， 每秒钟转出十种不同的组合， 也要花 1500 亿年的时间才能如愿 (作为比较， 我们的宇宙目前还不到 140 亿岁)。 与这样的组合数相比， 广告商们常用的 “成千上万”、 “数以亿计”、 “数以十亿计” 等平日里虚张声势、 忽悠顾客的形容词反倒变成了难得的谦虚。 我们可以很有把握地说， 假如不掌握诀窍地随意乱转， 一个人哪怕从宇宙大爆炸之初就开始玩魔方， 也几乎没有任何希望将一个色彩被打乱的魔方复原。

魔方与上帝之数

三阶魔方速拧世界纪录5.55s 三阶魔方速拧世界纪录5.55s 魔方的玩家多了， 相互间的比赛自然是少不了的。 自 1981 年起， 魔方爱好者们开始举办世界性的魔方大赛， 从而开始缔造自己的世界纪录。 这一纪录被不断地刷新着， 到本文写作之时为止， 复原魔方的最快纪录 - 如我们在本文开头提到的 - 已经达到了令人吃惊的 3.47秒。 当然， 单次复原的纪录存在一定的偶然性， 为了减少这种偶然性， 自 2003 年起， 魔方大赛的冠军改由多次复原的平均成绩来决定， 目前这一平均成绩的世界纪录为 5.80秒。 这些记录的出现， 表明魔方虽有天文数字般的颜色组合， 但只要掌握窍门， 将任何一种组合复原所需的转动次数却并不多。 那么， 最少需要多少次转动， 才能确保无论什么样的颜色组合都能被复原呢？ 这个问题引起了很多人， 尤其是数学家的兴趣。 这个复原任意组合所需的最少转动次数被数学家们戏称为 “上帝之数” (God's number)， 而魔方这个玩具世界的宠儿则由于这个 “上帝之数” 一举侵入了学术界。 要研究 “上帝之数”， 首先当然要研究魔方的复原方法。 在玩魔方的过程中， 人们早就知道， 将任意一种给定的颜色组合复原都是很容易的， 这一点已由玩家们的无数杰出纪录所示范。 不过魔方玩家们所用的复原方法是便于人脑掌握的方法， 却不是转动次数最少的， 因此无助于寻找 “上帝之数”。 寻找转动次数最少的方法是一个有一定难度的数学问题。 当然， 这个问题是难不倒数学家的。 早在二十世纪九十年代中期， 人们就有了较实用的算法， 可以用平均十五分钟左右的时间找出复原一种给定颜色组合的最少转动次数。 从理论上讲， 如果有人能对每一种颜色组合都找出这样的最少转动次数， 那么这些转动次数中最大的一个无疑就是 “上帝之数”。 但可惜的是， 4325 亿亿这个巨大的数字成为了人们窥视 “上帝之数” 的拦路虎。 如果采用上面提到的算法， 哪怕用一亿台机器同时计算， 也要超过一千万年的时间才能完成。 看来蛮干是行不通的， 数学家们于是便求助于他们的老本行： 数学。 从数学的角度看， 魔方的颜色组合虽然千变万化， 其实都是由一系列基本的操作 (即转动) 产生的， 而且那些操作还具有几个非常简单的特点， 比如任何一个操作都有一个相反的操作 (比如与顺时针转动相反的操作就是逆时针转动)。 对于这样的操作， 数学家们的军火库中有一种非常有效的工具来对付它， 这工具叫做群论 (group theory)， 它早在魔方问世之前一百四十多年就已出现了。 据说德国数学大师希尔伯特(D. Hilbert) 曾经表示， 学习群论的窍门就是选取一个好的例子。 自魔方问世以来， 数学家们已经写出了好几本通过魔方讲述群论的书。 因此， 魔方虽未成为空间几何的教学工具， 却在一定程度上可以作为学习群论的 “好的例子”。 对魔方研究来说， 群论有一个非常重要的优点， 就是它可以充分利用魔方的对称性。 我们前面提到 4325 亿亿这个巨大数字时， 其实有一个疏漏， 那就是并未考虑到魔方作为一个立方体所具有的对称性。 由此导致的结果， 是那 4325 亿亿种颜色组合中有很多其实是完全相同的， 只是从不同的角度去看 (比如让不同的面朝上或者通过镜子去看) 而已。 因此， 4325 亿亿这个令人望而生畏的数字实际上是 “注水猪肉”。 那么， 这 “猪肉” 中的 “水份” 占多大比例呢？ 说出来吓大家一跳： 占了将近 99%！ 换句话说， 仅凭对称性一项， 数学家们就可以把魔方的颜色组合减少两个数量级。 但减少两个数量级对于寻找 “上帝之数” 来说还远远不够， 因为那不过是将前面提到的一千万年的时间减少为了十万年。 对于解决一个数学问题来说， 十万年显然还是太长了， 而且我们也并不指望真有人能动用一亿台计算机来计算 “上帝之数”。 数学家们虽然富有智慧， 但在其它方面却不见得很富有， 他们真正能动用的也许只有自己书桌上的那台机器。 因此为了寻找 “上帝之数”， 人们还需要寻找更巧妙的思路。 幸运的是， 群论这一工具的威力远不只是用来分析象立方体的对称性那样显而易见的东西， 在它的帮助下， 新的思路很快就出现了。 革命尚未成功 目前只是找到了三阶魔方的上帝之数，但是4阶及以上，还有许多经典的异形的上帝之数还没有解决，看到三阶解决历程，可以想象找出所有魔方的上帝之数是对人类智慧的一大考验。

前端魔方模拟器threeJS

  • https://github.com/newbieYoung/Threejs_rubik
  • 知乎：threeJS
  • 作者博客
  • https://github.com/miniwangdali/SimpleRubiksCube
  • https://www.google.com/logos/2014/rubiks/iframe/index.html

min2phase和CubeExploer

  • http://kociemba.org/cube.htm 神一样的cube exploerer作者：两阶段算法
  • http://kociemba.org/twophase.htm
  • min2phase Java版代码：https://github.com/cs0x7f/min2phase
  • Github:kociemba算法C和Python接口
  • https://github.com/hkociemba/RubiksCube-TwophaseSolver

知乎

博客

史上最全的高阶魔方还原图文指导？

魔方网站

相信存在未知的算法巧妙的解决了目前人们认为不可能的问题

问题表面看上去十分复杂，似乎除了暴力解决没有任何解决方法，而实际上简单方法却经常是存在的。
就像一座大山，有很多条路到达山顶，但是常常存在一条很平坦很容易走的路。

要心存敬畏

人与人之间的差距是天壤之别的。有些人看一眼魔方就能够记忆住魔方的全部状态，然后盲拧解决魔方;有的人编出的程序既简短又迅速。
魔方需要记忆力，推理能力，空间想象能力，识别模式能力。

魔方只是小道

魔方只是一种谜题，像华容道，拼图，棋类一样，数独，数字谜题一样，浪费无数脑细胞在这上面并不值得，我们应该多研究一些经世致用的学问。
如果说魔方有用，那么可以研究一下华容道，华容道似乎更加艰难，操作序列更加难以捉摸。

删除脚手架

鸳鸯绣了从教看,莫把金针度与人.把与调试有关的代码删除掉,只保留最精简的部分.

二阶魔方

改变左下角前后两块的位置：下后下下后左后后左下左后后后左
改变左下角前后两块的状态：下后下下后下下左左下左后后后左后后后

三阶魔方

上左边块和左前边块状态改变公式：

后2下左2下下
左2左2左2
后2后2后2
左下下后2后2
左2左2下下
左2左2后2后2
下左左下

左面三边块交换位置：左上、左前、左下，三个边块位置轮转。

后2后2后2后
左2左2左2
下2下2左下2下2下2下
左左左下2下2
左2后2后2后后

三阶四面体魔方

左表示左2，右表示右2，下表示下1.

底部位置公式：
左、右逆、左逆、右

转脖子公式：
后后下左下，右右下后下

变两腰状态公式： 下下左下右左，右左下右下下