现在开始研究正方体魔方。
n阶正方体魔方由n^2-(n-1)^2个正方体小块组成,它有(n-1)*3种基本操作。固定魔方的最前,最右,最上角的一小块,可以执行下左后三类操作,每类操作有n-1种情况(表示转动几层)。
坐标系
魔方是三维空间中的立方体,三维空间有x,y,z三个轴,这三个轴分别用数字表示为0,1,2.
| 轴 | 数字 |
|---|---|
| x | 0 |
| y | 1 |
| z | 2 |
魔方的颜色
上下前后左右
白黄红橙绿蓝
用英语表示为white,yellow,red,orange,green,blue
简写为wyrogb
称之为"红心白发蓝右臂,黄足橙背绿左肩".
| 面 | 颜色 | English |
|---|---|---|
| 前面 | 红色 | Red |
| 后面 | 橙色 | Orange |
| 左面 | 绿色 | Green |
| 右面 | 蓝色 | Blue |
| 上面 | 白色 | White |
| 下面 | 黄色 | Yellow |
魔方的六个面
正方体有6个面,这是三维周正体的特点,二维中正方形4个边,四维中的周正体是正八体山.
这六个面分别以"前后左右上下"标识.
正方体可以展开成剑形:
上
左前右
下
后
"上左前右下后"分别编号为0,1,2,3,4,5
操作表示
对操作的编号=与该面垂直的轴的编号
对n阶魔方有三类操作:后,左,下。三类操作的编号分别为0,1,2.
x:0:后面旋转
y:1:左面旋转
z:2:下面旋转
操作序列举例:左2右3下2下下左左。左2表示旋转最左面的2层。这种操作序列表示法的好处在于可以表示任意一个n阶魔方。
魔方的操作
对于n阶魔方,固定离原点最远的那个小方块,则左边有n-1种旋转(只考虑单向旋转,因为逆向旋转可以通过三次单向旋转来实现),下边和后边也是有n-1种旋转.
这3*(n-1)种操作是最简操作集,最简操作集的意思是这些操作可以拼凑起其他操作,这些操作缺一不可,这就有点像矩阵里面秩的概念,矩阵的其他列向量都可以被基向量表示.
即对于n阶魔方,最简操作集包含3*(n-1)种操作,之所以是3是因为这是三维空间中的正方体,有下左后三个部分.如果是二维空间,则有下左两个部分。
当n=2时,最简操作集包含3种操作:左旋转,后旋转,下旋转.
相对于最简操作集,就有完备操作集.最简操作集和完备操作集都是不唯一的, 完备操作集包含的操作个数是最简操作集的二倍.
对于二阶魔方,至多有6种操作.顺时针右旋转相当于逆时针左旋转,所以二阶魔方的完备操作集为(顺+逆)*(左+后+下).
对于n阶魔方,把它的最简操作集加上顺逆即可构成完备操作集.例如三阶魔方最简操作集为6,完备操作集为12.最简操作集的一个例子为:上下前后左右六种顺时针选装.完备操作集的例子为(上下前后左右)*(顺逆).
n阶魔方的的属性
-
方块个数:
n^2-(n-1)^2 -
颜色面数:
n^2*6 -
基本操作个数: 3*(n-1)
-
状态个数:
奇数阶魔方状态总数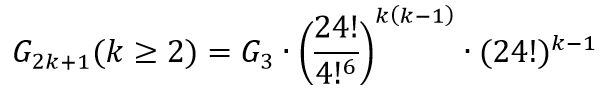 偶数阶状态总数
偶数阶状态总数
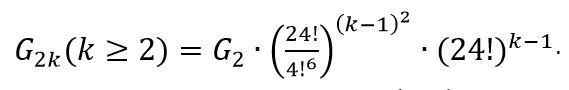
-
上帝之数:上帝之数跟操作集有关,目前广泛认同的上帝之数都是在完备操作集上。二阶魔方6种操作上帝之数是12,三阶魔方12种操作上帝之数是19。二阶魔方上帝之数可以暴力求解,因为二阶魔方的状态数很少,三阶魔方的上帝之数人们花了三十年才通过精巧的设计求出来,四阶魔方的上帝之数至今未知。
全色魔方
面魔方只考虑魔方的六个面,而不考虑魔方体内不可见的小方块,以上讨论的都是面魔方。
全色魔方认为魔方体内有小方块,这些小方块也是有颜色的。二阶魔方体内肯定没有小方块,三阶魔方体内的小方块是固定的,四阶魔方体内有一个二阶魔方,五阶魔方体内有一个三阶魔方。

全色魔方虽然不太直观,但是却是理论上很美观,实际上也可以制作的,利用镂空或者透明的方法就能看到里面的小魔方。面魔方跟全色魔方在二阶和三阶上是等价的。
正方体与内存表示的等价性
在计算机中,二维数组、三维数组等都可以理解为正方形、正方体。Python中的张量就是一个N维向量,而N维向量就可以理解为高维空间中的长方体。
二阶魔方相比二阶四面体魔方要简单一些,二阶四面体魔方编程解决起来略微复杂一点。